| 1.
Εισαγωγή
Το Δήλιον Πρόβλημα (δηλ. του υποδιπλασιασμού
του κύβου) και το πρόβλημα του Τετραγωνισμού του Κύκλου είναι τα
δύο περισσότερο γνωστά από όσα οι Αρχαίοι Έλληνες μαθηματικοί, γεωμέτρες
και φυσικοί επιστήμονες μας εκληροδότησαν ως άλυτα. Είναι, μάλιστα,
τα προβλήματα με τα οποία όλοι σχεδόν οι παραπάνω ασχολήθηκαν (άλλοι
με ένα εξ αυτών και πολλοί και με τα δύο).
Μαζί με αυτά, άλυτα (με την χρήση γνώμονα και διαβήτη) παραμένουν
και το πρόβλημα της τριχοτομήσεως της οξείας γωνίας και το συναφές
προς αυτό της κατασκευής κανονικών, εγγεγραμμένων πολυγώνων με δοθέντα
αριθμό πλευρών.
Το παρόν κείμενο ενδιαφέρει το
πρόβλημα του Τετραγωνισμού του Κύκλου (δηλ. της κατασκευής ενός
τετραγώνου ίσου εμβαδού προς δοθέντα κύκλον).
Η αξιολογότερη προσπάθεια, χάρις
στο πρακτικό ενδιαφέρον που παρουσιάζει, είναι αυτή του Ιππία του
Ηλείου. Αυτός φέρεται ότι ανακάλυψε καμπύλη, την οποία ονόμασε Τετραγωνίζουσα·
υπάρχουν, ωστόσο, κάποιοι που αμφισβητούν την πατρότητα, όπως παραπάνω,
και την αποδίδουν στον Δεινόστρατο τον Προκοννήσιο (τον αδελφό του
Μεναίχμου και φίλον του Πλάτωνος).
Ο Δεινόστρατος είναι, βεβαίως,
ο πρώτος που κατ' εξοχήν ασχολήθηκε με την αποδεικτικήν διαδικασία
των βασικών της σχέσεων έχοντας ως κύριον στόχο τον δι' αυτής τετραγωνισμό
του κύκλου· ως αποτέλεσμα τούτου διεσώθη (έμεινε περισσότερον γνωστή)
ως η Τετραγωνίζουσα του Δεινοστράτου.
Ο προαναφερθείς, συμφώνως με την
παράδοσιν, αναζητούσε μίαν τρίτη ανάλογο (δηλ. έναν επιπλέον λόγον
στην αναλογία της βασικής σχέσεως) η οποία θα έδιδε λύσιν στο πρόβλημα.
Πλην του Δεινοστράτου με την Τετραγωνίζουσα
ασχολήθηκαν, μεταξύ άλλων, και ο Αναξαγόρας ο Κλαζομένιος, ο Πάππος
ο Αλεξανδρεύς, ο Αρχιμήδης ο Συρακούσιος και ο Σπόρος.
Ο τρόπος κατασκευής της παραπάνω
καμπύλης, η απόδειξις της βασικής της σχέσεως καθώς και το πώς με
βάσιν αυτήν επιτυγχάνεται ο τετραγωνισμός του κύκλου, στην διατύπωσι
του οποίου δεν έφθασαν ο Ιππίας ή ο Δεινόστρατος (αν και το υποπτεύθηκε
ο αναφερθείς δεύτερος) αλλά ούτε ο μέγας Αρχιμήδης (εξ όσων, τουλάχιστον,
γνωρίζω) θα είναι τα θέματα που θα μας απασχολήσουν στην συνέχεια.

Σχήμα
1.
Σχήμα
2.
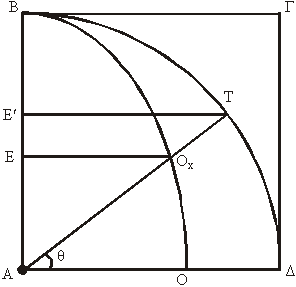
2. Η κατασκευή
(βλ. σχήμα 1ο)
α. Κατασκευάζουμε το τετράγωνο
ΑΒΓΔ.
β. Με ακτίνα την πλευρά ΑΒ και
κέντρο της το Α διαγράφουμε το τόξο του τεταρτοκυκλίου ΒΤΔ (ειδικότερα
υπό τις προϋποθέσεις, όπως περιγράφονται ακολούθως).
Θεωρούμε ότι η πλευρά ΑΒ (ακτίνα
ΑΤ) στρέφεται ισοταχώς κατά την φορά του βέλους μέχρι να συμπέσει
με την πλευρά ΑΔ και ταυτοχρόνως η πλευρά ΒΓ κατέρχεται ισοταχώς,
επίσης, ενώ παραμένει παράλληλος με την ΑΔ, μέχρι να συμπέσει με
αυτήν και ότι η κίνησις αμφοτέρων (των ΑΒ και ΒΓ) είναι εν συσχετίσει
τέτοια ώστε η σύμπτωσίς τους με την ΑΔ να είναι ταυτόχρονος.
Από τα σημεία της τομής τους (Ο1,
Ο2 κλπ.) θα γραφεί καμπύλη (η ΒΟ1Ο2Ο),
η οποία θα είναι ο γεωμετρικός τόπος των σημείων τομής των ΑΒ και
ΒΓ κατά την κίνησίν τους.
3. Η διερεύνησις
(βλέπε σχήμα 2ο)
α. Όταν
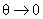 τα μήκη
τα μήκη
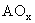 ,
,
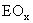 και ΑΟ τείνουν να καταστούν
ίσα.
και ΑΟ τείνουν να καταστούν
ίσα.
Ώστε, όταν οι πλευρές ΑΒ, ΒΓ και
ΑΔ συμπέσουν θα έχουμε ότι
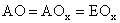 .
.
β. Από την συνθήκη της κατασκευής
συμπεραίνεται ότι:
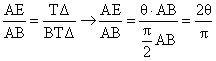 .
.
γ.
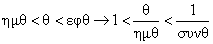 .
.
Όταν
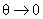 ,
,
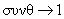 και άρα
και άρα
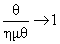 , επίσης.
, επίσης.
δ.
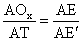 (εκ της ομοιότητος των τριγώνων).
(εκ της ομοιότητος των τριγώνων).
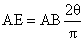 (όπως εδείχθη) και
(όπως εδείχθη) και
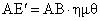 .
.
Σχήμα
3.
Συνεπώς
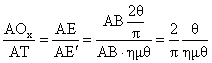 και
και
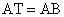 .
.
Έτσι προκύπτει η σχέσις συμφώνως
με την οποία η αξία του λόγου
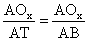 συναρτάται με την γωνία θ.
H θ λαμβάνει τιμές από
συναρτάται με την γωνία θ.
H θ λαμβάνει τιμές από
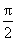 έως 0 ακτίνια.
έως 0 ακτίνια.
4. Η απόδειξις
της βασικής σχέσεως (βλέπε σχήμα 2ο)
Όταν
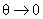 ,
,
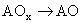 και
και
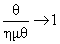 ώστε:
ώστε:
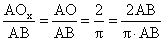 ,
,
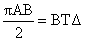 , δηλ. το τόξο του τεταρτοκυκλίου,
, δηλ. το τόξο του τεταρτοκυκλίου,
ώστε, τελικώς:
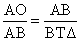 .
.
5. Ο τετραγωνισμός
(βλέπε σχήμα 3ο)
α. Αν φέρουμε την ευθεία
ΒΟ και την προεκτείνουμε μέχρι να συναντήσει την προς τα κάτω προέκτασιν
της πλευράς ΓΔ, θα κατασκευασθεί το ορθογώνιο τρίγωνο ΒΓΗ.
Τα τρίγωνα ΟΑΒ και ΒΓΗ είναι όμοια·
συνεπώς
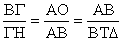
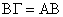 και
και
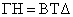 .
.
β. Αφού έτσι κατορθώθηκε η κατασκευή
του αναπτύγματος του τόξου του τεταρτοκυκλίου, ο τετραγωνισμός του,
και κατ' επέκτασιν του κύκλου, ανάγεται σε τετραγωνισμόν τριγώνου,
το οποίον, ως πρόβλημα, είναι απλό.
6.
Δευτερεύουσες εφαρμογές της Τετραγωνιζούσης
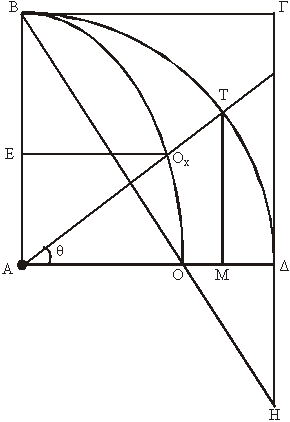
α. Η τριχοτόμησις της οξείας γωνίας (βλέπε σχήμα
4ο)
Έστω η οξεία ΤΑΔ. Εκ του σημείου
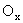 , στο οποίο η πλευρά ΤΑ τέμνει την Τετραγωνίζουσα, φέρουμε κάθετον
προς την ΑΒ· την
, στο οποίο η πλευρά ΤΑ τέμνει την Τετραγωνίζουσα, φέρουμε κάθετον
προς την ΑΒ· την
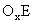 . Διαιρούμε, όπως δείχνεται, την ΑΕ σε τρία μέρη ίσα (ήτοι
. Διαιρούμε, όπως δείχνεται, την ΑΕ σε τρία μέρη ίσα (ήτοι
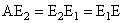 ) και εκ των σημείων
) και εκ των σημείων
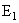 και
και
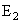 φέρουμε καθέτους προς την ΑΒ
και τις προεκτείνουμε μέχρις ότου συναντήσουν την Τετραγωνίζουσα στα
σημεία
φέρουμε καθέτους προς την ΑΒ
και τις προεκτείνουμε μέχρις ότου συναντήσουν την Τετραγωνίζουσα στα
σημεία
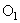 και
και
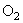 αντιστοίχως.
αντιστοίχως.
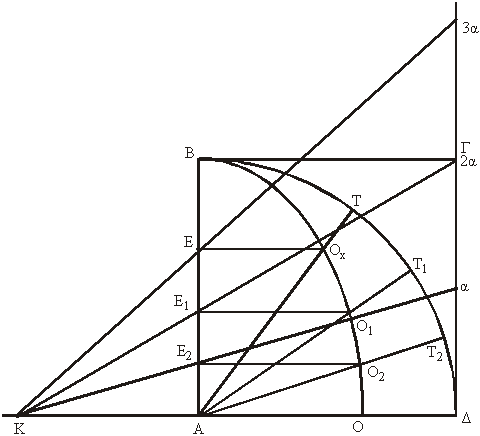
Σχήμα
4.
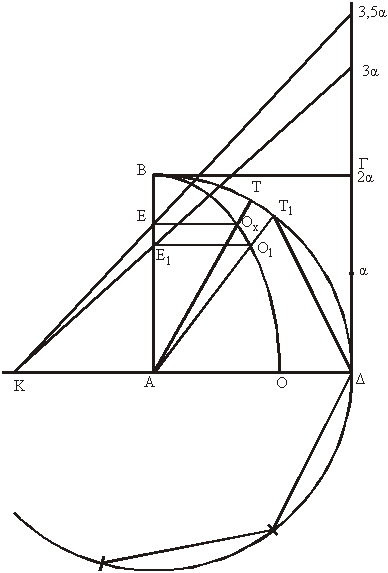
Σχήμα
5.
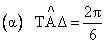 , ,
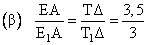 , ,
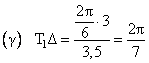
Ακολούθως φέρουμε τις ευθείες
 και
και
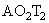 .
.
Είναι προφανές ότι οι γωνίες
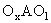 ,
,
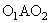 και
και
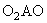 είναι ίσες ως βαίνουσες σε
ίσα τόξα (
είναι ίσες ως βαίνουσες σε
ίσα τόξα (
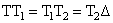 ).
).
β. Η κατασκευή κανονικών
εγγεγραμμένων πολυγώνων με δοθέντα αριθμό πλευρών (βλέπε
σχήμα 5ο)
Είναι φανερό ότι όχι μόνον η τριχοτόμησις
αλλά και η κατά βούλησιν διαίρεσις της οξείας γωνίας είναι δυνατή
με την χρήσιν της καμπύλης.
Ώστε είναι δυνατόν να κατασκευασθεί κανονικό πολύγωνο εγγεγραμμένο
σε δοθέντα κύκλο με τυχόν ζητούμενον αριθμό πλευρών με την κατάλληλον
διαίρεση της επικέντρου γωνίας άλλων γνωστών κανονικών πολυγώνων.
Στο σχήμα δείχνεται η κατασκευή κανονικού εγγεγραμμένου επταγώνου
δια διαιρέσεως της επικέντρου γωνίας του κανονικού εξαγώνου.
7.
Συζήτησις
α.
Η πλευρά ΑΒ δεν γίνεται παράλληλος με τις συνεχώς παράλληλες ΒΓ
και ΑΔ αφού τέμνεται με την ΑΔ στο σημείο Α· συμφώνως με το γνωστό
Ευκλείδειο αξίωμα δύο ευθείες σε ένα μόνον σημείο είναι δυνατόν
να τέμνονται.
Συνεπώς, το οποιοδήποτε σημείο
της
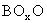 είναι σαφώς και απολύτως
προσδιορισμένο.
είναι σαφώς και απολύτως
προσδιορισμένο.
Το σημείον Ο αποτελεί το όριον των τομών κατά το πέρας της κινήσεως
(βλέπε σχήμα 1 και 2).
β.
Η ΓΗ είναι, προφανώς, η αναζητηθείσα από τον Δεινόστρατο
τρίτη ανάλογος.
γ.
Η καμπύλη, προφανώς, δεν μπορεί να κατασκευασθεί με τον κανόνα και
τον διαβήτη, όπως συμβαίνει και με άλλες καμπύλες αυτής της μορφής
(κογχοειδής, κισσοειδής κ.ά.).
8.
Συμπέρασμα
Η Τετραγωνίζουσα του Ιππία του
Ηλείου ή, όπως έχει επικρατήσει να αποκαλείται, η Τετραγωνίζουσα
του Δεινοστράτου όντως τετραγωνίζει τον κύκλο.
Βιβλιογραφία
1. Θ. Ματθαίου, «Η Τετραγωνίζουσα
του Ιππία του Ηλείου», Στρατιωτική Επιθεώρηση, τεύχος Φεβρουαρίου
1986.
2. Ε. Σπανδάγου, Ρ. Σπανδάγου, «Οι μαθηματικοί της Αρχαίας Ελλάδος»,
εκδόσεις ΑΙΘΡΑ, Αθήνα. |

